Funciones inyectivas, sobreyectivas y biyectivas.
http://www.slideshare.net/toribio99/funcin-inyectiva-sobreyectiva-biyectiva

• . Una función es inyectiva si cada f(x) en el recorrido es la imagen deexactamente un único elemento del dominio. En otras palabras, detodos los pares (x,y) pertenecientes a la función, y no se repiten.Para determinar si una función es inyectiva, graficamos la funciónpor medio de una tabla de pares ordenados. Luego trazamos líneashorizontales para determinar si las y (las ordenadas) se repiten ono.x –2 –1 0 1 2f(x) 2 –1 –2 –1 2Sea f una función de A en B, f es una función epiyectiva (tambiénllamada sobreyectiva), si y sólo si cada elemento de B es imagen deal menos un elemento de A, bajo f.A elementos diferentes en un conjunto de partida le correspondenelementos iguales en un conjunto de llegada. Es decir, si todoelemento R es imagen de algún elemento X del dominio.Ejemplo:A={a,e,i,o,u}B={1,3,5,7}

• 2. f={(a,1),(e,7),(i,3),(o,5),(u,7)}Simbólicamente:f: A B es biyectiva Û f es inyectiva y f es sobreyectivaSea f una función de A en B , f es una función biyectiva , si y sólo sif es sobreyectiva e inyectiva a la vez .Si cada elemento de B es imagen de un solo elemento de A,diremos que la función es Inyectiva. En cambio, la función esSobreyectiva cuando todo elemento de B es imagen de, al menos,un elemento de A. Cuando se cumplen simultáneamente las doscondiciones tenemos una función BIYECTIVA.Ejemplo:A={a,e,i,o,u}B={1,3,5,7,9}f={(a,5),(e,1),(i,9),(o,3),(u,7)}Teorema:Si f es biyectiva, entonces su inversa f - 1 es también una función yademás biyectiva.

UNA MANERA SIMPLE DE NO COMPLICARSE LA VIDA CON  LAS MATEMATICAS. Y SUS FUNCIONES
http://www.slideshare.net/JACQUELM/funciones-inyectivas-sobreyectivas-y-biyectivas

 FORMAS DE APRENDER MEJOR LAS FUNCIONES
http://www.youtube.com/watch?v=iSumT9bLbAQ

Ejercisios de funciones.

http://rinconmatematico.com/foros/index.php?topic=5576.0

FUNCIONES INYECTIVAS, SOBREYECTIVA Y BIYECTIVAS

http://es.scribd.com/doc/61012780/24/Funciones-inyectivas-sobreyectivas-y-biyectivas

PARA ENTENDER LAS FUNCIONES Y CON EJERCICIO

Inyectivo, sobreyectivo y biyectivo

"Inyectivo, sobreyectivo y biyectivo" te dan información sobre el comportamiento de una función.

Puedes entender una función como una manera de conectar elementos de un conjunto "A" a los de otro conjunto "B":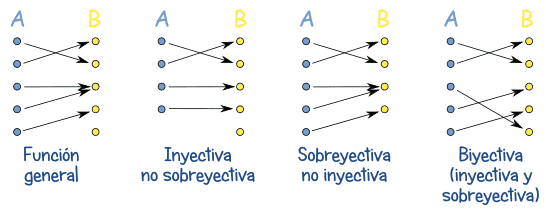

"Injectivo" significa que cada elemento de "B" tiene como mucho uno de "A" al que corresponde (pero esto no nos dice que todos los elementos de "B" tengan alguno en "A").
"Sobreyectivo" significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno).
"Biyectivo" significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.

Definiciones formales

Inyectivo

Una función f es inyectiva si, cuando f(x) = f(y), x = y.

Ejemplo: f(x) = x² del conjunto de los números naturales a es una función inyectiva.
(Pero f(x) = x² no es inyectiva cuando es desde el conjunto de enteros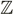 (esto incluye números negativos) porque tienes por ejemplo

• f(2) = 4 y
• f(-2) = 4)

Nota: inyectiva también se llama "uno a uno", pero esto se confunde porque suena un poco como si fuera biyectiva.

Sobreyectivo (o también "epiyectivo")

Una función f (de un conjunto A a otro B) es sobreyectiva si para cada y en B, existe por lo menos un x en A que cumple f(x) = y, en otras palabras f es sobreyectiva si y sólo si f(A) = B.
Así que cada elemento de la imagen corresponde con un elemento del dominio por lo menos.

Ejemplo: la función f(x) = 2x del conjunto de los números naturales al de los números pares no negativos es sobreyectiva.
Sin embargo, f(x) = 2x del conjunto de los números naturales a no es sobreyectiva, porque, por ejemplo, ningún elemento de va al 3 por esta función.

Biyectiva

Una función f (del conjunto A al B) es biyectiva si, para cada y en B, hay exactamente un x en A que cumple que f(x) = y
Alternativamente, f es biyectiva si es a la vez inyectiva y sobreyectiva.

Ejemplo: La función f(x) = x² del conjunto de números reales positivos al mismo conjunto es inyectiva y sobreyectiva. Por lo tanto es biyectiva.
(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo

• f(2)=4 y
• f(-2)=4)

<iframe width="560" height="315" src="http://www.youtube.com/embed/2-WlL1-Uz7Y" frameborder="0" allowfullscreen></iframe>

Este Blog esta dedicado a mi area de trabjo y los trabajadores de la contruccion, habilitacion, y remodelacion de tiendas de Retail.
En general la prevencion de riesgos ha evolucionado bastante, en especial por la responsabilidad social empresarial asociada a este tipo de construcciones.

Presento a continuacion algunos videos de accidentes en este tipo de trabajos.

Videos: